패리티 비트(Parity Bit)
시리얼 통신에서 데이터의 오류를 검출하기 위한 일종의 장치 중 하나입니다.
정보 전달 과정에서 오류가 생겼는지 검사하기 위해 추가하는 비트로 전송하고자 하는 데이터의 각 문자에 1비트를 더하여 전송합니다.
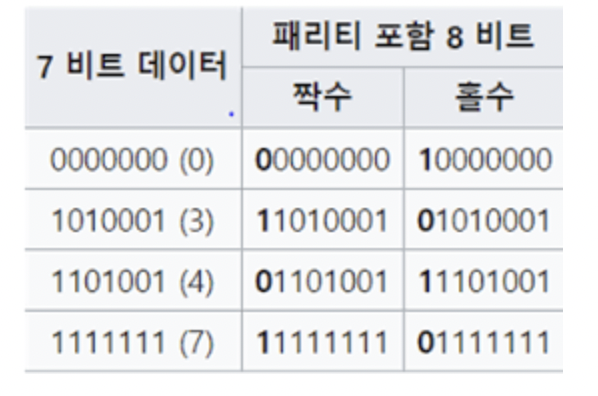
짝수 패리티
데이터의 모든 1의 개수를 짝수로 맞춰야합니다.
예를 들어, 1100100의 1의 개수는 3개(홀수)이므로, 자동적으로 패리티 비트는 1이 되어 11100100 총 1의 개수를 4개(짝수)로 만듭니다.
홀수 패리티
데이터의 모든 1의 개수를 홀수로 맞춰야합니다.
예를 들어, 1100100의 1의 개수는 3개(홀수)이므로, 자동적으로 패리티 비트는 0이 되어 01100100 총 1의 개수를 3개(짝수)로 유지합니다.
만약 짝수 패리티일 때, 데이터가 중간에 손실되어 11100100(1이 짝수) 이 아닌 11000100(1이 홀수) 가 가게 된다면 데이터가 손실 되었다는 것을 알 수 있습니다.
패리티 비트 특징
- 2비트의 데이터가 손실되면 알아차릴 수 없다.
- 오류를 검출만 할 뿐 수정하지 않는다.
해밍 코드
데이터 전송 시, 1비트의 에러를 정정할 수 있는 자기 오류 정정 코드를 말합니다.
패리티비트를 보고, 1비트에 대한 오류를 정정할 곳을 찾아 수정할 수 있습니다. (패리티 비트는 오류를 검출하기만 할 뿐 수정하지는 않기 때문에 해밍 코드를 활용합니다.)
패리티 비트 공식

위 식을 만족해야합니다.
p : 패리티 비트 추가 개수
n : 데이터 비트 개수
예를 들면, 14 라는 십진수는 이진수로 표현하면 1110 이고 데이터 비트 개수는 4개라고 할 수 있습니다.
따라서 패리티 비트 공식을 적용해볼 때 p = 3 이라고 가정하고 식에 대입해봅시다.

위 공식을 만족하기 때문에 데이터 비트가 4개일 때 패리티 비트를 3개 사용하면 해밍 코드를 사용할 수 있습니다.
이제 해밍코드 예제를 풀어보면서 익혀봅시다. (홀수 패리티 방식 사용)
우선 패리티 비트가 3개 이므로 2⁰, 2¹ ,2² 이 패리티 비트의 시작 자리가 됩니다. 또한 다음 비교표를 사용해야 홀수 패리티 방식을 사용할 수 있습니다. (비교표는 외워야하는 것 같습니다.)
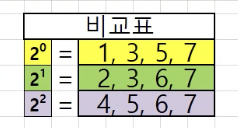
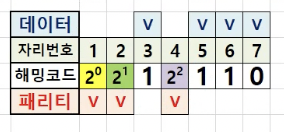
첫번째 1, 3, 5 ,7
위 예제를 볼때 자리번호 3 = 1 , 자리 번호 5 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트가 되려면 자리번호 1에는 1이 들어가야합니다.
따라서 자리번호 1의 해밍코드는 1로 채워집니다.
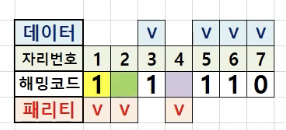
두번째 2, 3, 6 ,7
위 예제를 볼때 자리번호 3 = 1 , 자리 번호 6 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트가 되려면 자리번호 2에는 1이 들어가야합니다.
따라서 자리번호 2의 해밍코드는 1로 채워집니다.
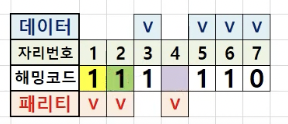
세번째 4, 5, 6 ,7
위 예제를 볼때 자리번호 5 = 1 , 자리 번호 6 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트가 되려면 자리번호 4에는 1이 들어가야합니다.
따라서 자리번호 4의 해밍코드는 1로 채워집니다.
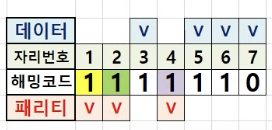
그럼 이제 위와 같은 제대로된 데이터를 아래의 3번째 자리 데이터를 0 으로 변경하여 오류 데이터를 만들어보겠습니다.
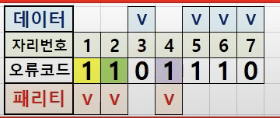
오류를 판단해보겠습니다.
첫번째 1, 3, 5 ,7
위 예제를 볼때 자리번호 1 = 1 자리번호 3 = 0 , 자리 번호 5 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트가 아닙니다.
아래와 같이 오류가 발생했으므로 1 을 표시합니다. (오류가 아닐때는 0)
두번째 2, 3, 6 ,7
위 예제를 볼때 자리번호 2 = 1 자리번호 3 = 0 , 자리 번호 6 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트가 아닙니다.
아래와 같이 오류가 발생했으므로 1 을 표시합니다. (오류가 아닐때는 0)
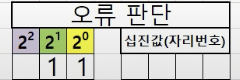
세번째 4, 5, 6 ,7
위 예제를 볼때 자리번호 4 = 1 자리번호 5 = 1 , 자리 번호 6 = 1, 자리번호 7 = 0 이므로 홀수개의 패리티 비트입니다.
아래와 같이 오류가 발생하지 않았기때문에 0 을 표시합니다.

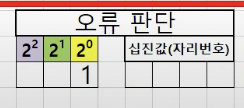
따라서 011 은 10진수로 3 이기 때문에 3번 자리에서 오류가 발생했다고 판단할 수 있습니다.
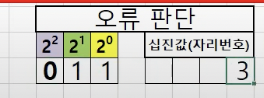
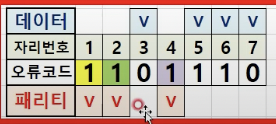
위 데이터에서 3번째 자리의 데이터는 0 이기 때문에 이것이 오류비트라면 정상 비트는 1 이 될 것입니다.
참고자료
1. https://dos-soles.tistory.com/20
2. https://www.youtube.com/watch?v=CLy9O81SXlU
'CS > 컴퓨터구조' 카테고리의 다른 글
| 리틀 엔디안(Little-endian) 과 빅 엔디안(Big-endian) 이란? (0) | 2023.04.14 |
|---|---|
| 명령어 집합 구조, CISC 와 RISC (0) | 2023.04.05 |
| CPU의 구조와 기능 (0) | 2023.04.04 |
| 컴퓨터 시스템의 개요 (0) | 2023.04.03 |
| 캐시 메모리의 쓰기 정책 / 버퍼와 캐시의 차이 (0) | 2023.04.02 |