문제 설명
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
- W, H : 1억 이하의 자연수
입출력 예
WHresult| 8 | 12 | 80 |
입출력 예 #1
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

https://programmers.co.kr/learn/courses/30/lessons/62048
w=7 H=12 일때, 7과 12는 서로소이기때문에 중간에 교점이 생기지 않을 것이라고 판단.
중간에 교점이 생기지 않는다.
망가진 사각형의 갯수 18개

w=6 , h=12 교점이 1:2 의 비율에서 생성된다.
망가진 사각형의 갯수 2(1:2 비율) * 6(6번 반복) = 12
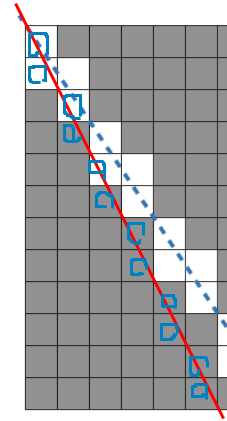
w = 5, h=12 중간에 교점에 생기지 않는다.
망가진 사각형의 갯수 16

w=4 , h=12 중간에 교점이 생긴다. 1:3 비율
망가진 사각형의 갯수 3(1:3 비율) * 4(4세트) = 12

최대공약수가 1이라면, 망가진 사각형의 갯수는 w+h-1 이 되고,
1이 아니라면, 망가진 사각형의 갯수는 최대공약수 * (w or h / 최대공약수) 일 것이다.
라고 생각 했는데 아니였다.
w=8 h=12 처럼 2:3 비율이 되는 케이스가 있었다.
이경우에는 최대공약수로 w/gcd =2 , h/gcd = 3 으로 만들어주고,
2,3 은 최대공약수가 1 이므로 w+h-1 공식을 써줘야되는 것이다.
결국에는 gcd 를 사용해서 사각형을 최대한 압축? 축소 시킨다음 비율을 얻고
축소시킨 사각형에서 w+h-1 공식을 사용하여, 부분적인 망가진 사각형의 갯수를 얻고
반복되는 횟수 * 부분적 망가진사각형 갯수
즉 , gcd * (w/a+h/a-1)해주면 전체적인 망가진 사각형의 갯수를 얻을 수 있다.
import math
def solution(w,h):
answer = 1
a = math.gcd(w,h)
break_square = (w/a+h/a-1)*a
square = w * h
answer= square - break_square
return answer
파이썬 최대공약수 , 최소공배수 구하는 메소드
https://blockdmask.tistory.com/525
[python] 파이썬 최대공약수, 최소공배수 함수 (gcd, lcm)
안녕하세요. BlockDMask입니다. 오늘은 파이썬에서 최대공약수와 최소공배수를 구할 수 있는 함수 gcd 함수와, lcm 함수에 대해서 알아보겠습니다. 파이썬에서는 정말 많은 게 함수로 되어있네요.
blockdmask.tistory.com
어제 같이 스터디하신분들의 해설을 들으니 이제야 보인다.
보이긴 무슨 답을 다 알아 놓고도 이렇게 오래걸리다니
어제 스터디 진행하면서 이문제에 40분을 소비했다.
오늘은 문제풀때, 최대 20분 정도 고민해보고 각이 안보이면 다음문제로
바로 넘어가야겠다.
'알고리즘 공부 > 미분류' 카테고리의 다른 글
| 프로그래머스 124 나라의 숫자 (0) | 2022.01.11 |
|---|---|
| 프로그래머스 3진법 뒤집기 (0) | 2022.01.11 |
| 백준 1730번 파이썬 (0) | 2022.01.06 |
| 플로이드 워셜 알고리즘 (0) | 2021.08.20 |
| 백준 1752번 with Kotlin (0) | 2021.08.20 |
